[DataAnalysis] PCA(Principal Component Analysis)

 

 

PCA(Principal Component Analysis)

: 여러 차원들의 특징을 가장 잘 설명하는 차원을 이용해 차원을 축소

 

 

 

1. 데이터 표준화 및 원점 이동

  1) 데이터 단위 통일(m, mm / g, kg)

  2) 데이터를 표준화(중심=원점을 기준으로 함)

 

 

 

 

 

2. 주성분 찾기

  1) 데이터의 중심(원점)을 지나고 모든 데이터들로부터 수직거리가 가장 가깝게 하는 선

  2) 주성분이 2개라면 두 번째 주성분 선은 첫 번째 주성분 선에 수직, 모든 데이터들에서 선까지 수직거리가 가장 작은 선      2-1) 주성분 찾는 방법

    : 데이터들의 분산이 최대가 되도록 하는 선(수직 거리 짧음)

    2-2) 두 번째 주성분 선이 첫 번째 주성분 선에 수직인 이유

    : 첫 번째 주성분과 비슷한 정보가 적음

 

 

 

 

 

3. 데이터 투영

  1) 모든 데이터를 각각의 선에 투영

 

 

 

 

 

4. 새로운 축 찾기

  1) 주성분 선을 새로운 축으로 함

= 두 개의 주성분 선이 각각 x축, y축이 되게 함.

 

- 후에 1차원으로 축소도 가능(새로운 x축(PC1))으로 투영

 

 

 

 

 

---

 

실습

- fit() 메소드 : 데이터를 통해 PCA를 학습

- transform() 메소드 : 학습된 PCA 모델을 바탕으로 데이터를 변환

 

 

# 모델 생성
pca = PCA(n_components=2)

pca.fit(scaled_df)  # PCA 학습
scaled_df_pca = pca.transform(scaled_df)  # PC로 데이터 변환
pca_df = pd.DataFrame(scaled_df_pca)  # 데이터프레임으로 변환

pca_df.columns = ['PC1', 'PC2']  # 데이터프레임 컬럼 이름 지정

pca_df.head()

 

 

 

 

시각화

sns.scatterplot(data=pca_df, x ='PC1', y='PC2')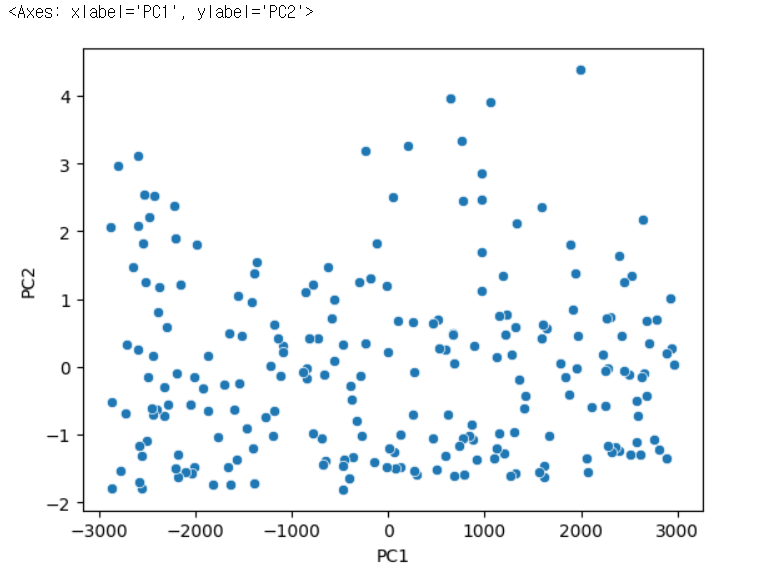

 

 

 

 

 

 

---

 

주성분의 수는 몇개로 해야할까?

• - 차원축소에는 Scree plot이 사용
• Scree plot은 각 주성분이 전체 데이터에 대해서 갖는 설명력 비율을 시각화한 플롯
• - Scree plot은 전체 주성분의 분산 대비 특정 주성분의 분산의 비율을 시각화 한 것

 

 

pca = PCA(n_components = 6)
pca.fit(scaled_df)  # PCA 학습
scaled_df_pc = pca.transform(scaled_df)  # PC로 데이터 변환
pca_df = pd.DataFrame(scaled_df_pc)
pca_df.columns = ['PC1', 'PC2', 'PC3', 'PC4', 'PC5', 'PC6']

pca_df.head()

 

 

 

→ 주성분의 분산 비율을 계산하기 위해서는 scikit-learn의 PCA에 있는 explained_variance_ratio_ 속성을 활용

import numpy as np
import matplotlib.pyplot as plt

# PCA 개수
num_components = len(pca.explained_variance_ratio_)

x = np.arange(num_components)
var = pca.explained_variance_ratio_ 

plt.bar(x, var) # Bar plot 그리기

plt.xlabel('PC')
plt.ylabel('Variance_Ratio')
plt.title('Scree plot')

plt.show()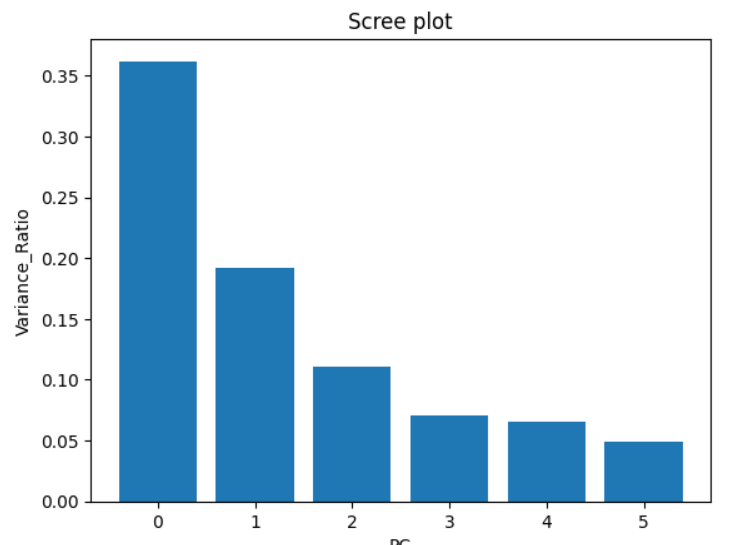

 

 

 

 

주성분의 누적 분산 비율

 

cum_var = np.cumsum(var)   # 누적 분산비율 구하기
cum_vars = pd.DataFrame({'cum_vars': cum_var}, index = pca_df.columns)

cum_vars

 

 

- 누적분산비율이 PC_N이 70%이상 되면 해당 개수가 주성분 개수

→ PC4까지로 주성분 결정